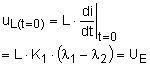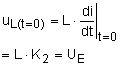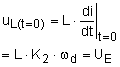Schaltvorgänge

Jede Energiezustandsänderung innerhalb eines beliebigen Systems erfordert eine endliche Zeit,
während der eine Energieform in eine andere umgewandelt wird.

Als Zustandsgröße wird dabei diejenige physikalische Größe bezeichnet, die den Energieinhalt
eines Energiespeichers beschreibt.

Der zeitliche Verlauf einer Zustandsgröße zwischen einem stationären Zustand und einem anderen
wird durch einen Übergangsvorgang gekennzeichnet. Je schneller dieser bei gleichem
Energieumsatz abläuft, desto größer ist die dabei auftretende Leistung.
 

·	um den Zeitverlauf jeder beliebigen mit einem Übergangsvorgang verknüpften Größe zu bestimmen, ist immer zuerst der Zeitverlauf der Zustandsgröße zu ermitteln
·	Zeitverlauf der Zustandsgröße und Struktur eines elektrischen Netzwerkes vor Beginn eines Übergangsvorganges sind ohne Bedeutung
·	der Anfangswert der Zustandsgröße (Index A) zum Schaltzeitpunkt t = 0 muss bekannt sein
·	zum Ende des Übergangsvorganges (t Þ¥ ) erreicht die Zustandsgröße einen stationären Endwert (Index E)

Schaltvorgänge bei Gleichspannung
 

lineares Netzwerk mit einer Kapazität	lineares Netzwerk mit einer Induktivität
Energie einer Kapazität (C = konst.): W = 0,5 × C × uC2 Zustandsgröße: uC	Energie einer Induktivität (L = konst.): W = 0,5 × L × iL2 Zustandsgröße: iL

Þ     Þ

jede Spannungsänderung ist gleichbedeutend mit einer Änderung des Energiezustandes, die Spannung ist Zustandsgröße  der Kapazität,  die Spannung an einer Kapazität  kann sich nicht sprunghaft ändern,

Þ     Þ

jede Stromänderung ist gleichbedeutend mit einer Änderung des Energiezustandes, der Strom ist Zustandsgröße  der Induktivität, der Strom durch eine Induktivität  kann sich nicht sprunghaft ändern

 

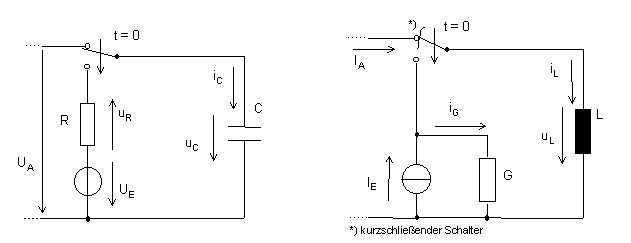
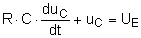
Maschengleichung (für t ³ 0): uR + uC - UE = 0 R × iC + uC = UE		Knotengleichung (für t ³ 0): iG + iL - IE = 0 G × uL + iL = IE
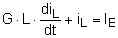
R × C = t	Zeitkonstante		G × L = t
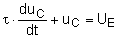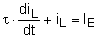DGL 1. Ordnung mit der allgemeinen Lösung: Trennung der Variablen
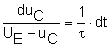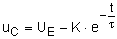
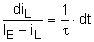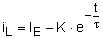
Integrationskonstante aus Anfangswert (bei t = 0)
der Spannung  uC(t=0) = UA = UE - K × e0	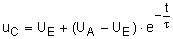	des Stromes  iL(t=0) = IA = IE - K × e0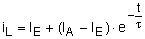

Der Übergangsvorgang wird aus der Summe zweier Teilvorgänge gebildet:
- der erste Therm repräsentiert einen konstanten stationären Endwert (t Þ¥ )
- der zweite Therm beschreibt einen Ausgleichs- oder transienten (flüchtigen) Anteil von
Spannung bzw. Strom
 

Besonderheit: Der Stromweg iL darf nicht plötzlich unterbrochen werden, da sich dann wegen 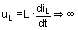ergibt: Verwendung eines kurzschließenden Schalters *)

Nachfolgendes Diagramm i = f (t) beschreibt die Vorgänge beispielhaft für eine R-L-Schaltung
(R = 50 W , L = 5 mH, t = 0,1 ms, I_A = 0 und I_E = 1 mA (0 £ t £ 0,5 ms), I_A = 1 mA und I_E = 0
(0,5 ms £ t £ 1 ms) :
(Anmerkung: die reale Zeit t = 0,5 ms im Diagramm erhält für den Übergangsvorgang erneut den Wert t = 0)
 

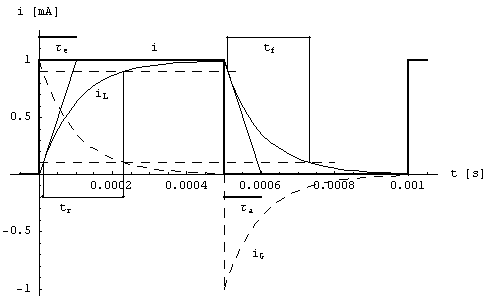
Die Zeitkonstante t kann durch Anlegen einer Tangente im Ursprung des Ausgleichsvorganges
der Zustandsgröße (hier: Strom i_L) als Länge der Subtangente in Höhe des Endwertes grafisch
bestimmt werden.

Nach Ablauf der Zeit t = 3×t werden beim Einschaltvorgang 95 % des Endwertes der Zustandsgröße
und nach t = 5×t  99 % dieses Endwertes erreicht, beim Ausschaltvorgang sinkt die Zustandsgröße
nach Ablauf dieser Zeiten auf 5 % bzw. 1 % des Anfangswertes:
Der Ausgleichsvorgang kann nach t = (3 ... 5)×t als abgeschlossen gelten.

Die Zeitspanne, die einer Differenz von 0,9× (Endwert - Anfangswert) und 0,1× (Endwert - Anfangswert)
entspricht, wird als Anstiegszeit t_r bzw. Abfallzeit t_f bezeichnet: t_r = t_f = 2,2×t .

Sind Anfangs- und Endwerte von Null verschieden, ergeben sich folgende nach einer Exponetialfunktion
verlaufende transiente Vorgänge:
Anfangswert < Endwert: Anstieg vom Anfangswert auf den Endwert,
Anfangswert > Endwert: Abfall vom Anfangswert auf den Endwert,
Anfangswert = Endwert: keine Änderung.

Ist der Zeitverlauf der Zustandsgröße bekannt, können damit die übrigen Netzwerkgrößen ermittelt werden:
 

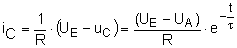
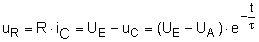
R - C - Schaltung: R × iC + uC - UE = 0 Der Zeitverlauf iC(t) ist bei t = 0 unstetig (Stromsprung !), er wird nur durch R begrenzt und ist als solcher nur bei Annahme einer vernachlässigbaren Induktivität in der Masche möglich. Das Vorzeichen der Spannungsdifferenz  UE - UA bestimmt die Stromrichtung. Die Spannung uR folgt dem Strom iC.

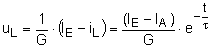
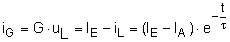
R - L - Schaltung: G× uL + iL - IE = 0 Der Zeitverlauf uL(t) ist bei t = 0 unstetig (Spannungsprung !), er wird nur durch  G = 1 / R begrenzt und ist als solcher nur bei Annahme einer vernachlässigbaren Kapazität am Knoten möglich. Das Vorzeichen der Stromdifferenz  IE - IA bestimmt die Spannungsrichtung. Der Strom iG folgt der Spannung uL.

lineares Netzwerk mit Widerstand, Induktivität und Kapazität (Schwingkreis)

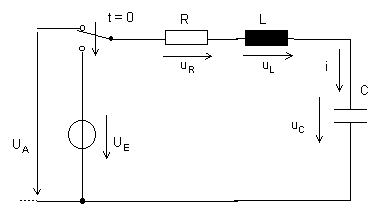
Maschengleichung:	uR + uL + uC = UE
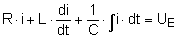
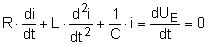
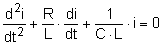Resonanzfrequenz:
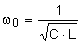Dämpfungsfaktor, Abklingkonstante:
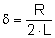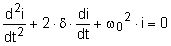charakteristische Lösung	l2 + 2×d×l + w02 = 0
mit
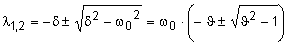Dämpfungsgrad
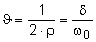Eigenfrequenz (für J < 1)
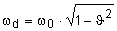Resonanzüberhöhung

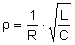Der Wurzelausdruck 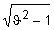 bestimmt das Verhalten des Schwingkreises während des
Übergangsvorganges. Es sind drei Fälle zu unterscheiden:
 

1. Aperiodischer Fall mit J > 1: l1 und l2sind reell, l1¹l2	2.Aperiodischer Grenz-  fall mit J = 1: eine reelle Lösung l1 = l2	3.Periodischer Fall mit J < 1: l1 und l2* sind konju- giert komplex
Die Zustandsgröße nähert sich ohne periodische Schwingung dem stationären Endwert, dieser wird um so schneller erreicht, je kleiner R ist.	Die Zustandsgröße nähert sich ohne periodische Schwingung dem Endwert in kürzest möglicher Zeit.	Die Zustandsgröße schwingt periodisch um den stationären Endwert bei gleichzeitiger exponentieller Abnahme der Amplitude (gedämpfte Schwingung, Dämpfung ist proportional zu R).
Anfangsbedingungen für UA = 0 (, IA = 0):
i(t=0) = 0 = K1 + K2 K1 = - K2	i(t=0) = 0 = K1	i(t=0) = 0 = K1
(- Strom kann sich wegen L nicht sprunghaft ändern)
uC(t=0) = uR(t=0) = 0

Die Lösung eines linearen Differenzialgleichungssystems bei mehreren vorhandenen
Zustandsgrößen (mehr als ein Energiespeicher in einem linearen Netzwerk) kann vorteilhaft
mit Hilfe der Laplace-Transformation erfolgen.

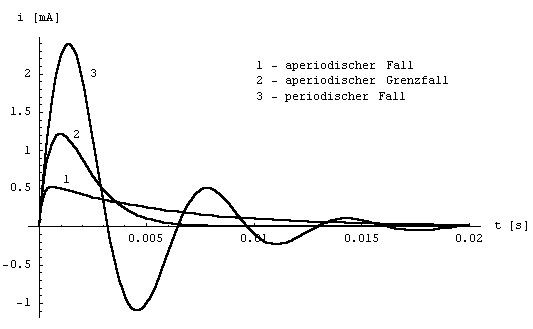
Nachfolgendes Diagramm i = f (t) beschreibt die Vorgänge beispielhaft für eine R-L-C-
Reihenschaltung bei U_A = 0 und U_E = 1 V mit
L = 0,3 H, C = 3,3 µF und

R =

1,8 kW

603 W

150 W

Berechnet werden:

Resonanzfrequenz w0 =	1005 s-1	1005 s-1	1005 s-1
Dämpfungsfaktor d =	3000 s-1	1005 s-1	250 s-1
Resonanzüberhöhung r =	0,167	0,5	2
Dämpfungsgrad J =	2,98	1	0,249
Eigenfrequenz wd =	-----	0	973,4 s-1
l1 =	- 5826,4 s-1	- 1005 s-1	(- 250 - j 973,4) s-1
l2 =	- 173,4 s-1	-----	(- 250 + j 973,4) s-1
Fall	aperiodisch	aperiodisch, Grenz-	periodisch

Die Spannungen der Zweipole R, L und C ergeben sich aus

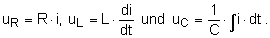
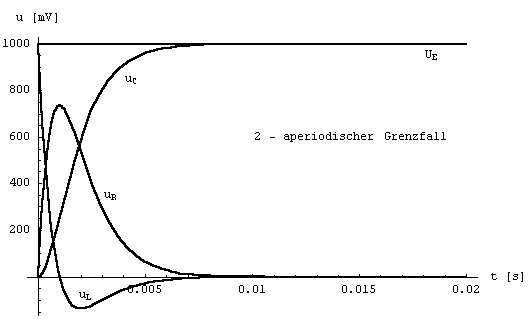
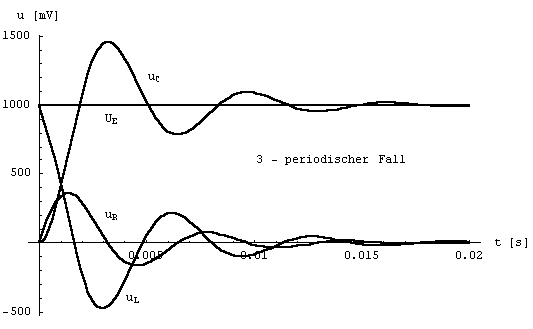
Für das Beispiel zeigen die folgenden Diagramme den Verlauf der Teilspannungen im
aperiodischen Grenzfall und im periodischen Fall:
 

Bearbeitung: JOT 05.02.01

(Quelle: HTW Dresden)